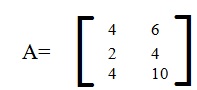How To Find The Base Of a Logarithm

Finding the base of a log is very simple.Before coming to the topic it is very important to

know the parts of a logarithm.The logarithm has three parts. Which are base, power and

exponent. If power and exponent are given in the problem, we can find the base.

For example: Logₓ 36=2

Here base is x, 36 is power, and 2 is exponent.

To find the base follow these four steps.

1.Write the given problem into exponential form.

First of all convert the logarithmic form into exponential form.

For Example:

Logₓ  16 = 2

x²=16

2. Convert the power into exponential form.

In our example the power is 16. So it will be equal to  4² or 2⁴.

x²=4²

3. Multiply the exponent of unknown base with its multiplicative

inverse on both sides.

The exponent of x is 2 in the above example. So its multiplicative inverse will be 1⁄2 .

(x²)1⁄2 =(4²)1⁄2

4. Solve the multiplication of the exponents to get the answer.

So exponent 2 and ½  will cancel each other and we will get our answer.

x=4

 So the base of the above logarithmic problem is 4.

How To Multiply a Matrix By 2 | Scalar Matrix Multiplication

How to multiply a matrix by a scalar

Do you know how to multiply a matrix by 2? Well, multiplying a matrix with number such as two is very easy. This kind of multiplication is called scalar multiplication. You can multiply any matrix of any order or dimension with any number whether it is whole number or real number, positive or negative.

To multiply a matrix by 2 there are three steps. First set the problem accordingly. Second multiply the given number with each entry in the matrix. Third write the result in the corresponding columns and rows.

We are going to learn how to multiply a matrix by 2.Look at (2) the number out of matrix or near the matrix or out of the bracket. This is the number we are going to multiply with numbers inside the matrix. We will multiply 2 with each number in matrix.

Keep in mind that there are three rows and two columns in the given matrix. So they will remain same when we get the answer. You can not get more rows and columns than the given number of columns and rows.

How to solve the problem?

We have to multiply the matrix A by 2 as given above.
Let’s solve the problem.

Step 1. Take 2 and multiply each number in the matrix with it.

Step 2. Now solve each multiplication.

That’s it. We have solved the matrix multiplication by 2.

How to multiply a matrix by a constant?

In matrices any real number you multiply with a matrix is called scalar value. So you can also say it a constant. It is very simple and easy to multiply a matrix by a constant. All you need is how to multiply two numbers, I am sure that you have already learnt multiplication of numbers.

Multiply a matrix by a constant is same as multiplying a matrix by 2. We have already solved this above. All the steps are same and simple.

Let’s take an example here. If

Then find 3B.

Solution of the problem:

you can say the given problem is how to multiply a matrix by 3. Here the constant number is 3. So we are going to multiply it with each element in the matrix B. You must observe the number of rows and columns.

Step 1. Set the problem.

Step 2.  Multiply 3 with each entry in the matrix.

Step 3.  Write the result of multiplication.

Now, I think, you have got it. If you have not don’t worry. We will solve further problems. Observe them and follow the steps.

How to multiply a matrix by a scalar?

Solving scalar multiplication is also same as multiplying a matrix by a constant. So it is going to be very easy to solve it.

Multiplying a matrix by a scalar value is not tough. All you have to do is set the given problem accordingly, multiply each digit in the matrix with the given scalar value, and write the result of product.

Before going further let’s learn definition of  Scalar multiplication.

What is scalar matrix multiplication?

Definition: Scalar matrix multiplication is defined as the product of a matrix with a scalar.( Source)

The term scalar multiplication states that it is the product of a real number and a matrix. (Source)
So you can say multiplication of a matrix by a real number is called scalar matrix multiplication.

Now take one more example.

If

Then find 5C.

Solving scalar matrix multiplication:

Here in this problem the scalar value is 5. To solve the problem we follow the steps below.

Step 1.

Step 2. 

Step 3. 

This is the answer. I hope you have understood all.If you are facing problem in calculation, you can use matrix multiplication calculator apps. I have written detailed post on ten best matrix multiplication calculator apps.

We have covered multiplication of a matrix by a real number, and a constant. in addition to this we also multiplied a matrix by a scalar, and learnt definition of scalar multiplication. 

I would love to answer your queries. Comment below if you have any question related to the topic.    

TOP TEN MATRIX MULTIPLICATION CALCULATOR APPS

Matrix multiplication calculators

Are you looking for best calculator app that solves multiplication step by step? Surely, you are. Continue reading this article, because we have brought top ten matrix multiplication calculator apps for you.

These matrix calculator apps are very helpful in solving matrices. Hence you can choose one of them.

Here are given those top ten matrix calculators.

1.Matrix Calculator by Alexander Skokov

This matrix calculating app is android based. It is completely free. The calculator app is only for matrix calculation.It solves not only matrix multiplication but also transposition of matrix and inverse of matrix.

Pros

1. It perform nearly all matrix operations: Multiplication, Addition, Subtraction, Inverse matrix, Determinant, Scalar multiplication, and Transpose matrix.

2. It supports integers, fractions ( decimal and common), and complex numbers.

3. This does not cost any money.

4. Very easy to use and understand.

5. Much better than others.

6. Very simple and quick
7. Performs fast matrix multiplication.

Cons

1. Does not support division.

2. Can not solve 6x6 matrix.

3. No integration and differentiation.

 2. Matrix Calculator by Softminds

                                                                                             

This is an open source project. Its slogan is matrix made easy. The app is android based. Both free and paid version are available.

Does this matrix multiplication calculator have variables?

Yes, it is matrix multiplication calculator with variables. You can add variables in the calculator.

Pros:

1. Performs all operations including exponentiation, first, second and infinity norm.

2. Can solve up to 9x9 matrix.

3. Can change name of matrix.

4. Advanced, allot of settings and easy.

5. Able to recall results.

Cons:

1. No complex numbers.

2. Can create 3 or 4 variables in free version.

3. Some device below 4.4 version are unable to create variable.  

3. Matrix Calculator by Koliuzhnov Viacheslay

This is another simple calculator with complete steps. Although it has ads, it is free.

Pros:

1. Solves all basic matrix calculations.

2. Can transpose a matrix.

3. Solution of system linear equation through Cramer's method is available.

4. Able to perform exponentiation in matrix.

5. Very easy and quick.

Cons: 

1. Free version contains ads.

2. Exponent functions needs a fix.

4. Linearibus - Matrix Calculator by Kedamp

The tool is very useful and helpful to students. The matrix calculator solves multiplication along with determinant and inverse. Besides that it solves system of linear equations.

Pros:

1. Solves reverse matrix by Gauss-Jordan method.
2. Multiplies matrix with steps.
3. Find inverse matrix by determinant method.
4. Calculates trace of matrix.

Cons:

1. Uses comma instead of  decimal point.
2. Has ads.

 How does the matrix calculator work?

Operating this calculator is very easy. Check out the video which shows how to operate it.

5. Matrix Calculator by Kartollika

The matrix application is very handy for students who want to solve matrix problems. It is very easy and contains all operations you need.

Pros:

1. Supports rational numbers.

2. High accuracy.

3. Night theme for using at night.

4. You can solve both scalar multiplication and multiplication of two matrices.

Cons:

1. Stores only two matrices.

2. Annoying ads.

6. Matrix Super Scientific Calculator by NTsoft apps      

This is also another free android application for matrix calculations. It performs nearly all operations and has lots of features. You would love to use it.

Pros:

1. Works with integers, fractions, and decimals.

2. You can operate matrix co-factors and matrix rank.

3. Row-wise operation of matrix Gaussian elimination.

Cons:

1. Some bugs in determinant and Adjoint calculations.

2. Theme looks poor.

To take an overview of android matrix calculator play the video below.

7. Matrix Calculator (Matrices with details by STEMath

This matrix calculator is perfect for students who study linear Algebra and matrices. Along with answer it shows detailed calculation.

Pros:

1. Provides null space computation.

2. Supports eigenvectors calculation.

3. Does Gram-Schmidt normalization.

4. Uses fractions.

Cons:

1. Too many annoying ads.

2. To get the result you have to watch ads.

Watch the video to see how it solves matrix multiplication with steps.

8.Matrix Operations by ONE DAY OF CODE

Multiplying matrix is simple and easy through this amazing matrix app. You can calculate all matrix problems in the calculating app.

Pros:

1. It has auto convert fraction option.

2. Presents you customized keyboard.

3. Helps you in LU decomposition.

Cons:

1. Does not support 6x6 matrix.

2. You can use fractions.

3. Needs improvement.

9. Square Matrix Calculator by shaikh roshan

Square matrix calculator is very simple matrix calculating app. It solves only square matrix and performs addition, subtraction, and multiplication.

Pros:

1. Very simple for multiplication of square matrix.

2. Easy and simple interface.

3. Supports 4x4 matrix.

Cons:

1. Does not have 5x5 matrix.

2. You can not perform scalar multiplication.

10.Scientific Matrix Calculator by Daniel Di Capua

Scientific matrix calculator as the name suggest is very great app for engineering students. It performs a large number of operations. The calculator facilitates writing and editing of long expressions with great typography.

Pros:

1. Able to store expressions.

2. Supports Greek letters.

3. Capable of zoom in and zoom out.

4. Generates user defined functions.

5. Provides complex numbers.

Cons:

1. Some devices face installation problems.

2. Bugs need fixation.

3. Requires 8.1 or more android versions.

Conclusion:
Calculators really help when you are learning math. We discussed best ten matrix calculator apps that do multiplication. We learnt that the android based apps perform a lot of operations besides multiplication. We recommend you to choose one of them according to your need.

If you want to learn multiplication of matrix, check our article how to multiply a matrix by 2. We have written detailed post on scalar matrix multiplication. 

6 SIX TRIGONOMETRIC RATIOS: How To Find Ratios in Trigonometry?

Trigonometry is a branch of mathematics.It shows relation of an angle with ratio of two side of a right triangle. Every right triangle has 6 trigonometric ratios.

1. Sine (sin)

2. Cosine (Cos)

3. Tangent (Tan)

4. Secant ( Sec)

5. Cosecant ( Cosec)

6. Cotangent ( Cot)

Each of the ratios has specific formula, which are given below:

Trigonometric formulas of 6 ratios:

Definition of trigonometric ratios 

Ratio is defined as a relation between two things. Trigonometric ratios represent relation between two sides of a right triangle.

Definition of Sine: Sine is the ratio of the opposite side of the angle and hypotenuse. Opposite side of the given angle divided by hypotenuse of a right triangle is called sine.

Definition of Cosine: Adjacent side of the given angle divided by hypotenuse of a right triangle is called Cosine,

Definition of Tangent: Opposite side of the given angle divided by adjacent side of the given angle of a right triangle is called Tangent.

Definition of Cotangent: Adjacent side of the given angle divided by opposite side of the given angle of a right triangle is called Cotangent.

Definition of Secant: Hypotenuse divided by adjacent side of the given angle of the right triangle is called Secant.

Definition of Cosecant: Hypotenuse divided by opposite side of the given angle of a right triangle is called Cosecant.

How to find the trigonometric ratios of a right triangle?

To find trigonometric ratios follow  five steps below.

1. Select the ratio you want to find.
 For example you want to find ratio of Sin.

2. Which angle to use.
It is very important to keep in mind which angle you are going to use. Because adjacent and opposite sides depend on it.
If given angle is Ө, use it in the ratio.Write it as Sin Ө.

3. Identify the sides ( Hypotenuse, Adjacent, and Opposite).
Find sides according to the given angle. 

4. Substitute formula of the selected ratio.
Let's suppose opposite side of Ө is b and hypotenuse is c. So substitute the formula with the values in right triangle.

5. Solve the ratio.
Finally solve the ratio if it need further calculation.
In above example the ratio of Sin Ө will be:
Sin Ө = b / c

 You must to know the formulas of  trigonometric ratios to find the ratios.

Let's find out the ratios of following triangle.

 You have noticed that angle of the ratios is B which is represented by θ. So in that case opposite side of angle B is b and adjacent side of angle B is a.

What is hypotenuse?

Hypotenuse is opposite side of right angle.Here right angle is C,hence hypotenuse is c.

Let's solve another example.

 In this triangle we have found ratios according to angle A.

Practice Problem:

Find out the following ratios according to angle B in the above right triangle.

1. Sin B

2.Cos B

3. Tan B

4. Cot B

5. Sec B

6. Cosec B

Answers

Logarithm Formula or Logarithm Rules

Logarithm is inverse of exponent.To solve problem related to logarithm you need to know its rules or properties.Without these rules you can not solve logarithm problems.To have all the rules of logarithm at one place would be very helpful for you.These all logarithm formula or logarithm rules are given below for your reference.

All Algebra Formulas

Algebra is a branch of Mathematics. It uses letters and numbers.Multiple formulas are used to solve problems in Algebra.You need all formulas in one place for reference.We have collected all formulas for you.Here are all Algebra formulas.

1. Factoring Formulas:

2. Product Formulas:

3. Powers in Formulas:

4. Roots Formulas:

For more formulas read math 8 formula sheet.

How to use Algebra Formulas?

To use Algebra formulas go through following examples.

1. 4a² - 9 = (2a)² + (3)2
               = (2a + 3)(2a - 3)

2. (5y + 3)² = (5y)² + 2(5y)(3) + (3)² 
                   = 25y²  + 30y + 9

3. (49)²  = (50 - 1)² 
              = (50)² - 2(50)(1) + (1)² 
              = 2500 - 100 + 1
              = 2401

4. (a²  )²  = a⁴

5. ⁴ ___
     ⎷625 = (5*5*5*5)¹⁄ ⁴
              = (5⁴)¹⁄ ⁴
              = 5